Graph
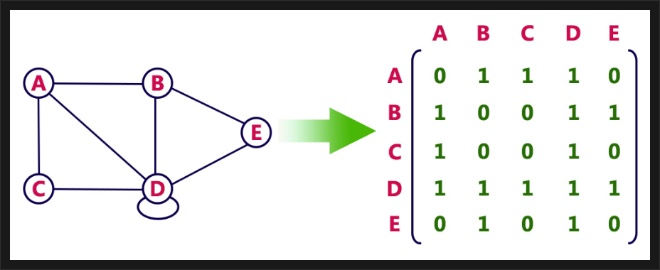
그래프 자료구조를 나타내는 방법으로 두 가지가 있다. 하나는 인접 행렬 (adjacent Matrix) 이고 하나는 인접 리스트 (adjacent List)법이있다. 이번 글에서는 인접행렬로 그래프를 나타내는 방법을 알아보겠다. 인접행렬법은 배열로 그래프를 나타내는 것이므로 밀집그래프 (완전그래프)를 표현하는데 적절하다. 2차원 배열 특성상 한번에 메모리를 잡아햐 하기때문에 빈 공간이 생기면 메모리 낭비가 생기므로 밀집그래프를 표현하는데 있어 좋은 방법이다.
(※무방향 그래프를 표현 시 대칭성을 고려해야 한다.)
Implementaion
Define
extern int check[];
/*----------------------------------------------
GraphMatrix 처리 구조체 및 활용 함수
-----------------------------------------------*/
typedef struct
{
int graph[MAX_VERTEX][MAX_VERTEX]; /* 인접 행렬법 표기 배열 - 2차원 배열 */
int vertexCnt; /* 정점 개수 */
int edgeCnt; /* 간선 개수 */
}GraphMatrix;
void initGraph(GraphMatrix *gm, char *fileName); /*데이터파일에서 그래프의 정점과 간선 정보를 입력 받아 그래프를 초기화하는 함수 */
void outputGraph(GraphMatrix *gm); /* 그래프내의 정점과 간선의 관계를 인접 행렬 형태로 출력 함 */
void DFS_Matrix(GraphMatrix *gm); /* 여러 개의 연결 요소로 구성된 그래프를 깊이 우선 탐색하기 위한 함수(재귀판) - DFS_recursive()함수를 호출하여 처리(이 함수 자체는 재귀하지 않음) */
void DFS_recursive(GraphMatrix *gm, int vNum); /* 연결되어있는 하나의 그래트내의 모든 정점을 재귀호출기법으로 방문하는 함수 */
void visit(int vNum); /* 방문한 정점의 처리 */
void nrDFS_Matrix(GraphMatrix *gm); /* 여러 개의 연결 요소로 구성된 그래프를 깊이 우선 탐색하기 위한 함수(비 재귀판) */
void BFS_Matrix(GraphMatrix *gm); /* 여러 개의 연결 요소로 구성된 그래프를 너비 우선 탐색하기 위한 함수(비 재귀판) */
int countGraphComponents(GraphMatrix *gm); /* 인접 행렬법으로 표기되 그래프 내의 연결 요소별로 정점들을 출력하고 연결 요소의 개수를 리턴하는 함수 */
extern 전역 변수로 방문처리를 확인 할 1차원 배열을 하나 선언해준다. ( 0번방 -> A , 1번방 -> B… 이런 식) 구조체에는 인접행렬을 표기할 배열 graph 2차원 배열, 정점의 갯수와 간선의 갯수를 저장해줄 int형 변수들을 선언해준다.
Init graph
void initGraph(GraphMatrix *gm, char *fileName)
{
FILE *pFile = fopen(fileName, "r");
char str[3];
if (pFile == NULL)
printf("불러오기 실패\n");
else
{
fscanf(pFile, "%d", &gm->vertexcnt); // 정점갯수 가져옴
fscanf(pFile, "%d", &gm->edgeCnt); // 간선갯수 가져옴
for (int i = 0; i < gm->vertexcnt; i++) // 배열 방 '0' 으로 초기화
for (int j = 0; j < gm->vertexcnt; j++)
gm->graph[i][j] = 0;
for (int k = 0; k < gm->edgeCnt; k++)
{
fscanf(pFile, "%s", str);
str[0] = str[0] - 65; str[1] = str[1] - 65; // ex) str[3] = { 0 , 1 }
gm->graph[str[0]][str[1]] = 1;
gm->graph[str[1]][str[0]] = 1;
}
}
}
이 글에서는 행렬 텍스트 파일을 파일입출력을 통해 불러와 반복문을 통해 배열에 입력하는 방식으로 구현했다. FILE 함수를 통해 파일을 읽어들인 후, 간선, 정점의 갯수를 모두 읽는다.
우선, 인접행렬영역을 0 (방문X)로 초기화를 해주고, 무방향 그래프에서의 대칭성을 고려하여 간선의 갯수만큼 반복문을 이용해 행렬에 입력한다.
Print graph
void outputGraph(GraphMatrix *gm)
{
printf(" ");
for (int k = 0; k < gm->vertexcnt; k++)
printf(" [%c]", 65 + k);
NEWL;
for (int i = 0; i < gm->vertexcnt; i++)
{
printf("[%c]", 65 + i);
for (int j = 0; j < gm->vertexcnt; j++)
printf("%5d", gm->graph[i][j]);
NEWL;
}
}
DFS
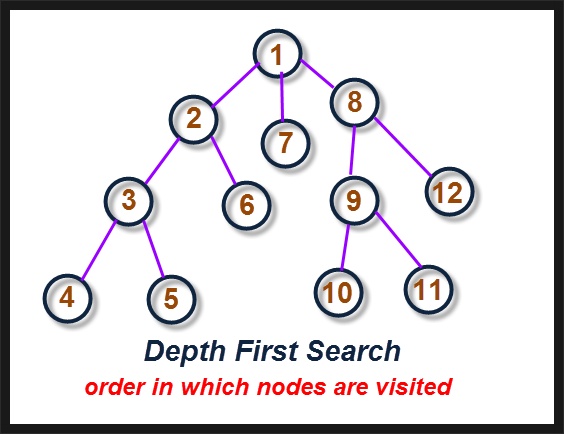
그래프내의 각 정점들을 간선을 타고 중복없이 한 번씩 방문하는 방법으로 깊이 우선 탐색 ( Depth First Search ) 법과 너비 우선 탐색 ( Breadth First Search)법이 있다. 무방향 그래프는 특성상 방향이 없기때문에 순회 순서가 유일하지 않다는 특징이 있다.
2가지 중 하나인 “깊이 우선 탐색(DFS)” 는 탐색을 시작할 정점에 연결된 정점 중 하나를 선택하여 들어가고 그 하나와 연결된 정점들 중 또 하나를 선택해서 들어가고 깊이 들어가는 방식으로 탐색하는 기법이다.
DFS의 과정은 스택을 사용하므로 재귀와 비재귀로 구현 할 수 있다
Recursive dfs
void DFS_recursive(GraphMatrix *gm, int vNum)
{
int i;
check[vNum] = 1; /* 방문한 정점 표시를 위해 1 저장 */
visit(vNum); /* 방문에 따른 처리 */
for(i=0; i<gm->vertexCnt; ++i)
{
if(gm->graph[vNum][i] != 0) /* 연결된 정점이 있으면 */
if(check[i] == 0) /* 또한 방문한 적이 없는 정점이면 */
DFS_recursive(gm, i); /* 재귀 호출을 통해 정점 방문을 한다 */
}
}
전달인자로 받은 정점번호를 방문처리 해준 뒤, ( 1로 바꿈 ) 그 정점을 visit함수 ( 출력 ) 한다. 다음으로, 정점갯수만큼 반복문을 설정.. 해당 정점에 연결된 정점이 있고 그 정점이 방문배열에서 방문한 적이 없는 정점 이라면 재귀호출을 통해 정점 방문 처리를 해준다.
Non-Recursive dfs
void nrDFS_Matrix(GraphMatrix *gm)
{
int i, j;
int popData; /* pop한 데이터 저장 */
Stack stack;
initStack(&stack); /* 비재귀 처리를 위해 사용될 스택 초기화 */
for(i=0; i<gm->vertexCnt; ++i) /* 정점의 방문상태 정보를 저장할 check배열 초기화 */
check[i] = 0;
for(i=0; i<gm->vertexCnt; ++i) /* 순차적으로 정점을 방문함 */
{
if(check[i] == 0) /* 방문하지 않은 정점을 발견 하면 */
{
push(&stack, i);
check[i] = 1; /* 방문상태를 1로 변경 */
while( !isStackEmpty(&stack) ) /* 스택이 비면 한 연결 요소에 대한 순회가 끝난것을 의미함 */
{
pop(&stack, &popData);
visit(popData); /* 정점 방문 */
for(j=0; j<gm->vertexCnt; ++j)
if(gm->graph[popData][j] != 0) /* (!!)pop한 정점과 연결된 j정점이 있고 */
if(check[j] == 0) /* j정점이 스택에 들어있지 않으면 */
{
push(&stack, j); /* j정점을 스택에 저장하고 */
check[j] = 1; /* 방문상태를 1로 변경 */
}
}
}
}
destroyStack(&stack);
return;
}
재귀기법을 사용하지 않으면 스택자료구조를 이용해야한다. 스택 초기화 및 생성을 하고 재귀방법과 똑같이 체크배열은 0으로 시켜준다. 순차적으로 정점을 방문한다. 그 정점이 방문한경우가 아니라면 스택에 그 정점을 푸쉬하고 방문상태를 바꿔준다 ( 1로 ) 그리고 스택이 모두 비면 한 연결 요소에 대해 순회가 끝난것을 의미하므로 스택이 빌 때까지 반복문을 걸어준다. pop을 하여 정점을 꺼내고 해당 정점에 연결된 정점이 있고 방문처리 되지 않은 경우 그 인접정점을 스택에 넣고 방문처리를 해준다. 이런 과정을 모두 하고나면 모든 정점에 대해 순회가 완료된다.
BFS
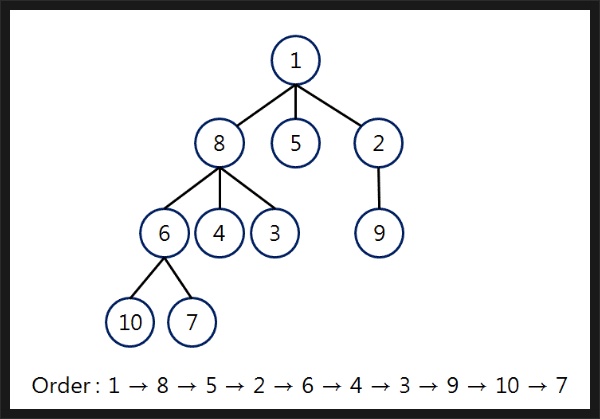
너비우선탐색 (BFS) 는 시작한 정점과 연결된 모든 정점을 탐색하고 다시 시작 정점의 다른 연결된 정점을 찾는 순으로, 깊이 들어가기전에 옆으로 넓게 퍼지며 탐색하는 기법이다. DFS와 달리 너비우선탐색 (BFS) 는 스택을 사용하지않고 큐 자료구조를 이용해야 한다. 따라서 재귀호출기법으로는 구현할 수 없다.
void BFS_Matrix(GraphMatrix *gm)
{
int i, j;
int getData; /* dequeue(get)한 데이터 저장 */
Queue queue;
initQueue(&queue, MAX_VERTEX); /* 큐 초기화 */
for(i=0; i<gm->vertexCnt; ++i) /* 정점의 방문상태 정보를 저장할 check배열 초기화 */
check[i] = 0;
for(i=0; i<gm->vertexCnt; ++i) /* 순차적으로 정점을 방문함 */
{
if(check[i] == 0) /* 방문하지 않은 정점을 발견 하면 */
{
enqueue(&queue, i);
check[i] = 1; /* 방문상태를 1로 변경 */
while( !isQueueEmpty(&queue) ) /* 스택이 비면 한 연결 요소에 대한 순회가 끝난것을 의미함 */
{
dequeue(&queue, &getData);
visit(getData); /* 정점 방문 */
for(j=0; j<gm->vertexCnt; ++j)
if(gm->graph[getData]j] != 0) /* (!!)pop한 정점과 연결된 j정점이 있고 */
if(check[j] == 0) /* j정점이 스택에 들어있지 않으면 */
{
enqueue(&queue, j); /* j정점을 스택에 저장하고 */
check[j] = 1; /* 방문상태를 1로 변경 */
}
}
}
}
destroyQueue(&queue);
return;
}
과정은 DFS랑 매우 비슷하다. 자료구조만 스택에서 큐로 바꾸면 바로 너비우선탐색법이 된다.
큐를 선언 및 초기화 후 체크배열을 초기화한다. 그리고 시작 정점을 기준으로 하여 큐에 넣고 큐가 빌때까지 반복문, 인접정점, 방문 유무를 판단한다. [그림 3] 을 예로들어서 설명하면 “1"을 시작으로 Enqueue한뒤, “1"의 인접정점 8 , 5, 2 를 순서대로 모두 Enqueue한다. 그리고 Dequeue를 하면 큐 특성상 첫번째로 넣은 값이 나오게 되므로 8을 방문처리하고 8의 인접정점 6 ,4 ,3 을 모두 Enqueue 그 다음 5를 Dequeue… 5는 인접정점이 없으므로 다음 Dequeue 2를 방문…이런 식으로 옆으로 넓게 퍼지며 탐색을 한다.
print graph
int countGraphComponents(GraphMatrix *gm)
{
int componetsCount=0; /* 그래프 내의 연결 요소 카운트 변수 */
int i, j;
int popData; /* pop한 데이터 저장 */
Stack stack;
initStack(&stack); /* 비재귀 처리를 위해 사용될 스택 초기화 */
for(i=0; i<gm->vertexCnt; ++i) /* 정점의 방문상태 정보를 저장할 check배열 초기화 */
check[i] = 0;
for(i=0; i<gm->vertexCnt; ++i) /* 순차적으로 정점을 방문함 */
{
if(check[i] == 0) /* 방문하지 않은 정점을 발견 하면 */
{
++componetsCount; /* 방문하지 않은 정점을 발견되면 연결 요소 카운트를 증가 시킴 */
printf("\n연결 요소 %d : ", componetsCount);
push(&stack, i);
check[i] = 1; /* 방문상태를 1로 변경 */
while( !isStackEmpty(&stack) ) /* 스택이 비면 한 연결 요소에 대한 순회가 끝난것을 의미함 */
{
pop(&stack, &popData);
visit(popData); /* 정점 방문 */
for(j=0; j<gm->vertexCnt; ++j)
if(gm->graph[popData][j] != 0) /* (!!)pop한 정점과 연결된 j정점이 있고 */
if(check[j] == 0) /* j정점이 스택에 들어있지 않으면 */
{
push(&stack, j); /* j정점을 스택에 저장하고 */
check[j] = 1; /* 방문상태를 1로 변경 */
}
}
}
}
destroyStack(&stack);
return componetsCount;
}